Punktweise Konstruktion der Ableitungsfunktion
Die nachfolgend dargestellte Methode kann sehr leicht bei vorgegebenem Funktionsgraph von Hand durchgeführt werden.
Eine Ableitungsfunktion wird dabei punktweise erzeugt:
An einer beliebigen Stelle x0 auf der x-Achse kann im zugehörigen Kurvenpunkt (Punkt T) die Tangente t angelegt werden. Diese Tangente wird parallel durch den Punkt E (-1/0) verschoben und schneidet die y-Achse dann in einem Punkt F. Die beiden Koordinatenachsen bilden mit EF ein Steigungsdreieck. Da die Strecke OE die Länge 1 hat, entspricht die Strecke OF gerade dem Wert der Ableitung an der Stelle x0. Diese Länge wird nun an die Stelle x0 zurückverschoben, wodurch wir den Kurvenpunkt P der Ableitungsfunktion an der Stelle x0 erhalten.
Durch Variieren der Stelle x0 überstreicht der Punkt P den Graph der Ableitungsfunktion.
Durch Variieren der Stelle x0 überstreicht der Punkt P den Graph der Ableitungsfunktion.
Nachfolgend betrachten wir die Funktion y = sin(x).
Nachfolgend betrachten wir die Funktion 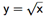 .
.
Erstellt mit GeoGebra von Fortunat Schmid